Simplificación de la suma y resta de fracciones algebraicas
Con igual denominador
Suma:
En este caso, se mantiene el denominador y se opera con los numeradores. Podemos dejar una sola fracción con el denominador común y con los términos de ambos numeradores:
Y después agrupar términos semejantes en el numerador:
Tenemos el mismo denominador y por tanto, podemos unir todos los numeradores en uno sólo. Pero ahora, delante de la última fracción tenemos un signo menos. esto afecta a los dos términos del numerador de la fracción que tiene detrás. Por tanto, para que siga siendo así, los términos afectados por el signo menos deben ir encerrados entre paréntesis:
Obtenemos el denominador común calculando el mínimo común múltiplo de los denominadores.
Por ejemplo, tenemos sumas y restas de fracciones algebraicas, cuyos denominadores no son iguales:
El primer paso será reducirlas a denominador común calculando el mínimo común múltiplo de los denominadores:
Para ello, previamente, hay que descomponer los polinomios.
Los polinomios de la segunda y la tercera fracción algebraica no se pueden descomponer por ser de grado 1. Descomponemos el denominador de la primera fracción y nos queda:
Luego resolvemos como una suma y resta de fracciones normal, dividimos el denominador del resultado por el denominador del ejercicio, y luego todo eso lo multiplicamos para el numerador del ejercicio, lo cual de respuesta nos dará sumas o restas depende del ejercicio.
Entonces volviendo al ejercicio veamos:
Quedaría así una vez sacado el m.c.m
Luego dividimos cada fracción por el m.c.m
Hacemos lo misma con todas hasta obtener:
Ahora ya podemos unir todos los numeradores en una sola fracción con el denominador común. Ten en cuenta, como siempre, que el signo menor afecta a todos los términos del numerador que tiene detrás y por eso, debemos encerrar esos términos entre paréntesis
Eliminamos el paréntesis del numerador:
Agrupamos términos en el numerador y en el último paso, multiplicamos en el denominador para obtener el resultado final:



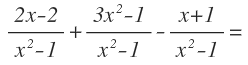


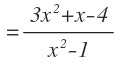


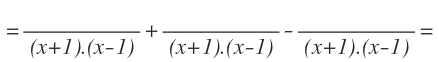


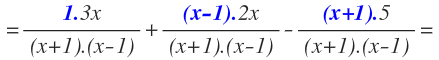




Comentarios
Publicar un comentario