¿Qué son los productos notables?
Los productos notables están íntimamente relacionados con fórmulas de factorización, por lo que su aprendizaje facilita y sistematiza la solución de diversas multiplicaciones, permitiendo simplificar expresiones algebraicas complejas.
1. Cuadrado de un Binomio
Introducción: Newton es el creador del binomio de newton, un producto notable que resuelve a suma o la resta de dos binomios al cuadrado. Se llama producto al resultado de una multiplicación, y los valores que se multiplican se llaman factores
Fórmula: Es igual al cuadrado del primer término, más el doble producto del primer termino por el segundo término, más el cuadrado del segundo término
En la suma todos los signos son positivos, pero es la resta son intercalados empezando por menos.
Ejemplos:(x + 3)2 = x 2 + 2 · x ·3 + 3 2 = x 2 + 6 x + 9
(2x − 3)2 = (2x)2 − 2 · 2x · 3 + 3 2 = 4x2 − 12 x + 9
Ejercicios de práctica:
(a+2)³ = a³ +3(a²)(2) +3(a)(2²) +2³ = a³ +6a² +12a +8
Al igual que en el cuadrado de un binomio, en la suma todos los signos son positivos, pero es la resta son intercalados empezando por menos.
(n-4)³= n³ – 3(n²)(4) + 3(n)(4)² – 4³
= n³ -12n² +48n -64
Ejercicios de práctica: https://www.matesfacil.com/ESO/newton/ejercicios-resueltos-cuadrado-de-la-suma-binomio-de-newton.html
3. Producto de la suma por la diferencia
“Suma por diferencia es igual a diferencia de cuadrados". Es decir, que el resultado de multiplicar la suma de dos números por su diferencia es el mismo que si restamos los cuadrados de ambos números
Fórmula: La suma por la diferencia de dos términos es igual a la diferencia de los cuadrados de dichos términos
(a + b) (a - b) = a2 - b2
Ejemplos:
Ejercicios de práctica:
4. Producto de dos binomios con un término en común
Los binomios con un término común, son aquellos binomios donde uno de los dos términos que integran cada binomio, es igual en ambos.
Fórmula: (x+a)(x+b) es igual al cuadrado del termino común, más el producto de la suma de los dos términos no comunes por el término común, más el producto de los término no comunes.
Ejemplo:
(x + 2) (x + 3) =
= x2 + (2 + 3)x + 2 · 3 =
= x2 + 5x + 6
Ejercicios de práctica:
Video sobre los Productos Notables:
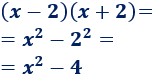
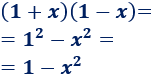
Comentarios
Publicar un comentario